Surface electron states @ MOLPIT

Surface electron states

Information to support the article: Denisov I.A., Zimin A.A., Bursill L.A., Belobrov P.I. Nanodiamond collective electron states and their localization // Journal of Siberian Federal University. Mathematics & Physics. 2014. Vol. 7 (1). P. 35–45.

Permanent URL for this page is: http://tammstates.molpit.org

Surface States Explorer v1.1

Consider the model of one-dimensional dielectric crystal, bounded on both sides by vacuum. The potential of such an array is created by atoms nuclei, electrons constitute the inner molecular orbitals and the electrons that are involved in the covalent bond. The calculation of the potential of such a system is currently unsolvable task for large systems, so for simplicity we use the model of the Kronig-Penney, and the approach of a test electron in this potential. In a very rough approximation, we can assume that the one-dimensional crystal will have the following contour.

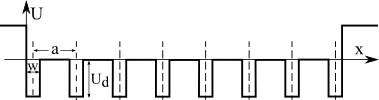
Potential of limited one-dimensional crystal in Kronig-Penney approximation

Lets solve one-dimensional stationary Schroedinger equation for chosen potential:

$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+U(x)\psi(x)=E\psi(x)$

Lets choose numerical grid with nodes in points 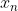$x_n$ and exchange the second derivative in that equation according to the next equation:

$\frac{d^2 y(x)}{dx^2}=\frac{y_{n-1}-2y_n+y_{n+1}}{h^2},$

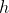where $h$ — space step, 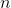$n$ — number of nodes in grid, so:

$- \frac{\hbar^2}{2m}\frac{y_{n-1}-2y_n+y_{n+1}}{h^2}+U_ny_n=Ey_n,$

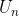where $U_n$ — value of potential energy 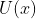$U(x)$ on grid nodes.

For convenience we introduce the typical scale of the potential $a$ , in our case it is convenient to take it's value of 1 Å. This means that the step h = 0.1 corresponds to 0.1 Å. Then, after the transformation we can write the previous equation in dimensionless form:

$-y_{n-1}+\left(2+h^2\frac{2ma^2U_n}{\hbar^2}\right) y_n-y_{n+1} = h^2\frac{2ma^2E}{\hbar^2}y_n.$

If we label the dimensionless values of potential energy and eigenenergies as:

$v_n = \frac{2ma^2U_n}{\hbar^2} \qquad e = h^2\frac{2ma^2E}{\hbar^2},$

a dimensionless equation can be written as system of equations:

$- y_{n-1} + (2 + h^2 v_n - e) y_n-y_{n + 1} = 0.$

In matrix form this equation will be:

$ \begin{bmatrix} 2+h^2v_1&-1&0&\dots&0\\ -1&2+h^2v_2&-1&\dots&0\\ \hdotsfor{5} \\ 0&\dots&-1&2+h^2v_{N-1}&-1\\ 0&\dots&0&-1&2+h^2v_N \end{bmatrix} - e E = 0 $

Thereby, the problem of search of stationary wave functions is equal to problem of search of eigenenergies and eigenvectors for that three-diagonal matrix.

To find the eigenvalues QL algorithm was used (Numerical Recipes in FORTRAN Edition 2, p.469) from mathematical subsystem Lib. After finding the eigenvalues, eigenvectors were computed with tridiagonal matrix algorithm.

For the implementation of numerical algorithms, visualization of graphics and studies of the quantum system under different boundary conditions the application in BlackBox Component Builder have been written.

Obtained representative solution demonstrates surface (subsurface) electron localization.

Bands structure of one-dimensional limited crystal shows that there are two degenerate electron state between valence band (HOMO) and conductivity band (LUMO).

If we take more deep potential, there are several valence bands, and we can also see more unoccupied molecular orbitals. In this hight-energy bands surface states are also exists. That states skip from one band to other if we change lattice constant.