To be write in English later. Today is importent that Hilbert's 13th problem

Сегодня, 13/01/13 можно анонсировать теорему, связанную тесно с 13-й проблемой Гльберта, с хопфионом и с диполиком.

Теорема. "Солитон Хопфа (хопфион) является примером функции, которую нельзя представить в виде суперпозиции функций меньшего числа переменных".

Примечание. Существует вариант введения вместо 3-х декартовых 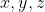, 3-х сферических 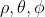и т.п. координат следующих трёх переменных: кривизна, кручение, зацепление, в которых хопфион имеет "естественное" (математическое, логическое или физическое) представление (выражение).

Подсказка. Нами был предложен вариант представления хопфиона путем разбиения трехмерного пространства 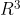на бесконечное число попарно зацепляющихся всех со всеми окружностей Вилларсо. Существует много точно эквивалентных математических описаний естественного физического выражения "попарное зацепление бесконечного числа окружностей, одна из которых ось Z". Первое описание было сделано нами в 1991 году в препринте: http://molpit.org/files/61_Dipolic1991.pdf

По поводу существования функций 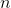переменных, которые нельзя представить в виде суперпозиции функций от меньшего числа переменных (на физическом языке - существование функций, для которых нельзя сделать разделения переменных), лучше всего прочесть статью: А. Г. Витушкин. 13-я проблема Гильберта и смежные вопросы // УМН, 59 #1 (355), 11–24 (2004). Витушкин2004; Vitushkin2004.

Это последняя статья Анатолия Георгиевича Витушкина, которого не стало 9/5/2004. Выдающийся математик, ученик Колмогорова. В связи с 13-й проблемой Гильберта он показал, что почти всякая гладкая функция не может быть представлена суперпозицией функций такой же гладкости от меньшего числа переменных. Для хопфиона это факт принципиальной значимости. Рекомендую прочесть его статью и самим убедится в интеллекте Анатолия Георгиевича. На сайте МИАН: Витушкин Анатолий Георгиевич (1931–2004) можно прочесть подробнее о его вкладе в науку.