Исследователь многоуровневых систем v.1.5 @ Blog MOLPIT

DIA00097 Исследователь многоуровневых систем v.1.5

#многоуровневые системы #модель связей #приложения #блэкбокс

После анализа моего автореферата PIT и ZIM пришли к выводу, что я должен привести все рассчитанные диаграммы с указанием размерностей энергии, времени и начальных системы. Поэтому пришлось вспомнить и изучить новые приемы обезразмеривания и восстановления размерностей DIA00095, а также прикинуть реальные коэффициенты упругости DIA00096.

Итак встречайте:

Исследователь многоуровневых систем 1.5.3

Пример расчета

Для примера промоделируем образование связи между двумя объектами атомных масштабов. Возьмем два атома углерода, и из условия, что при сближении появляется объект организации, который притягивает атомы.

Динамика многоуровневой системы описывается следующим гамильтонианом DIA00069:

$\left\lbrace \begin{aligned} H = & \sum_{i,j} \mathcal{T}_j^i \left( \frac{(p^i_j)^2}{2m^i_j} + \sum_{k \neq i} \mathcal{T}_j^k \frac 1 2 U_j^L (q^i_j, q^k_j) +\right.\\ & + \sum_{k \not\in D^i_j} \mathcal{T}_{j+1}^k \frac 1 2 U_j^{L+1} (q^i_j, q^k_{j+1}) + \sum_{k \not\in P^i_j} \mathcal{T}_{j-1}^k \frac 1 2 U_j^{L-1} (q^i_j, q^k_{j-1}) + \\ & \left. + \sum_{k \in P^i_j} \mathcal{T}_{j-1}^k \frac 1 2 U_j^P (q^i_j, q^k_{j-1}) + \sum_{k \in D^i_j} \mathcal{T}_{j+1}^k \frac 1 2 U_j^D (q^i_j, q^k_{j+1}) \right), \end{aligned}\right.$

где $j$ — номер уровня организации; $i$ — номер объекта организации на уровне; $q_j^i$ — координаты $i$ -ого объекта организации на уровне $j$ ; $p_j^i$ — импульс $i$ -го объекта на уровне $j$ ; $m_j^i$ — масса $i$ -го объекта на уровне $j$ ; $U_j^L$ — потенциал взаимодействия между объектами уровня $j$ ; $U_j^{L+1}$ — объектами уровней $j$ и $j+1$ ; $U_j^{L-1}$ — объектами уровней $j$ и $j-1$ ; $U_j^P$ — объектов уровня $j$ c родительскими объектами уровня $j-1$ ; $U_j^D$ — объектов уровня $j$ c дочерними объектами уровня $j+1$ ; $P^i_j$ — множество родительских объектов для $i$ -го объекта уровня $j$ ; $D^i_j$ — для $i$ -го объекта уровня $j$ .

Выберем потенциалы, триггер и сукцессор соответствующие постановке задачи:

$\left\lbrace \begin{aligned} U_j^L &= 1000 \left(\left( (r_i^j + r_i^k)/(q_i^j - q_i^k)\right)^{12}-2\left((r_i^j + r_i^k)/(q_i^j - q_i^k) \right)^{6}\right),\\ U_j^P &= U_j^D = 500 \, (q_i^j - q_i^k) / 2, \qquad U_j^{L-1} = U_j^{L+1} = 0,\\ \mathcal{T}_j^i & = \Theta\left(\sum_{m,n \neq m, \lbrace n, m \rbrace \nsubseteq D^n_{j-1}, \lbrace n, m \rbrace \nsubseteq D^m_{j-1} } \sqcap\left( \frac{q^n_{j-1} - q^m_{j-1}}{r^n_{j-1} + r^m_{j-1}}\right) \right.\\ & - \left. \sum_{m \in P^n_{j},n \in P^n_{j} } \sqcap\left( \frac{q^n_{j-1} - q^m_{j-1}}{1.1(r^n_{j-1} + r^m_{j-1})}\right) \right),\\ \mathcal{S}_j & = (\mathcal{O}_j^n + \mathcal{O}_j^m) \left( \begin{array}{cc} 1/2 & 0 \\ 0 & 1/2 \end{array} \right), \quad \mathcal{O}_j^i = \left(\begin{array}{cc} m_j^i & r_j^i \end{array}\right). \end{aligned}\right.$

В результате расчета в приложении Levels 1.5 получим результат, изображенный на рисунке 1. Слева без диссипации энергии, справа с учетом диссипации 0.1 Па с.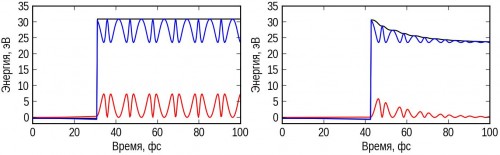

Рис. 1. Расчет согласно уравнению выше, с массой объектов 12 а.е.м., радиусом — 1 ангстрем, начальным расстоянием между центрами 3 ангстрема, коэффициент жесткости для возникающего объекта 500 кг/c²

Ivan Denisov 08 Dec 2013 14:52