ПИД-регулятор для поддержания темепературы @ Blog MOLPIT

DIA00215 ПИД-регулятор для поддержания темепературы

Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса.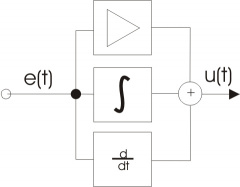

Для настройки коэффициентов ПИД-регулятора требуется сначала получить периодический отклик при воздействии на систему управляющим воздействием $u$ пропорционально некоторому коэффициенту $K_u$ умноженному на разницу целевого $T_t$ и текущего $T(t)$ значений температуры (ошибку).

$u(t) = K_u (T(t) - T_t)$

Далее $(T(t) - T_t)$ на шаге $n$ обозначим как $e_n$ .

Тут $u(t)$ — это мощность условного нагревателя или элемента Пельтье в случае охлаждения системы. Далее $u(t)$ на шаге $n$ обозначим как $u_n$ .

Однако, если процесс ассиметричный, к примеру, остывание системы быстрее чем нагрев, то необходимо учесть поправку к этой ошибке $e_n$ перед исследованием периода колебаний.

Для определения поправки, охладим систему на максимальной мощности, и потом дождёмся, когда она вновь нагреется.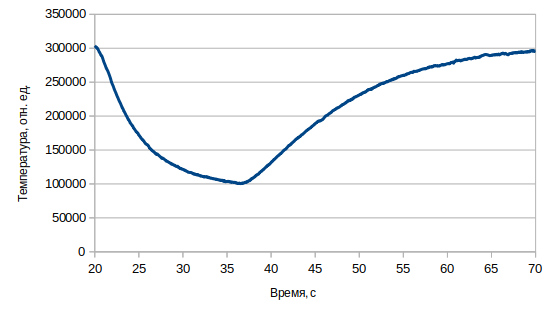

Так примерно мы сможем определить разницу в характерных временах для двух напревлений процесса и умножать либо делить разницу $(T - T_t)$ на коэффициент. В нашем случае коэффициент примерно будет равен 2.

$\tilde e_n = 2 \cdot e_n$

Теперь нам надо найти 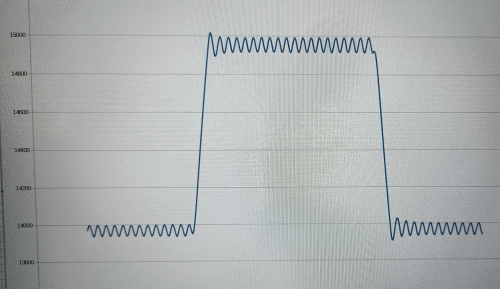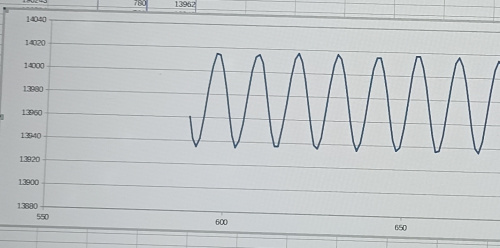$K_u$ такой, чтобы при управляющем воздействии получить гармонические колебания.

Для нашей системы $K_u$ был равен 105. При этом период колебаний $T_u$ составил 1,1 c.

Тогда согласно теории для управляющего воздействия на шаге $n$ справедливо следующее соотношение:

$u_n = K_p (\tilde e_n + T_d (\tilde e_n - \tilde e_{n-1}) / dt + K_{ip} \sum_0^n \tilde e_n dt)$ ,

где

$K_p = 0,6 \cdot K_u$

$T_d = 0,125 \cdot T_u$

$K_{ip} = 2 / T_u$

Формула содержит как дифференциальную часть, где учитывается разница ошибки на текущем и предыдущем шаге, так и интегральная накопительная ошибка.

В виде программного кода в прошивке прибора данный алгоритм реализован следующим образом:

    PROCEDURE SetPeltPWM (data: INTEGER);
    CONST
        dt = 0.1;
        delKp = 2.0;
        Ku = 105.0;
        Tu = 1.1;  (*  1.1 c *)
        Kp = 63.0;  (*  Ku * 0.6 *)
        Td = 0.1375;  (* Tu * 0.125  *)
        Kip = 1.818;  (*  1 / (0.5 * Tu)  *)
    VAR
        e, u: REAL;

    BEGIN
        currentTemp := data;
        e := FLT(data - temp);
        IF e > 0.0 THEN (* температура ниже заданной *)
            e := e * delKp
        ELSE
            e := e / delKp
        END;
        eInt := eInt + e;
        u := Kp * (e + Td * (e - ePr) / dt + Kip * eInt * dt);
        ePr := e;
        u := - u;
        coolPWM := FLOOR(u) + 4000;
        IF coolPWM < 0 THEN
            coolPWM := 0;
            eInt := eInt - e;
        ELSIF coolPWM > 7999 THEN
            coolPWM := 7999;
            eInt := eInt - e;
        END;
        PWM.SetTIM5(1, coolPWM);
    END SetPeltPWM;

После применения данной формулы для ПИД-регуляции прибор стал выходить на рабочий режим менее чем за 10 секунд:

Ivan Denisov 01 Mar 2023 07:11