Сложность кляксы и энергия химсигнала @ Blog MOLPIT

PIT00105 Сложность кляксы и энергия химсигнала

Немного о кляксе (стр.183-185 Belobrov1996 (djvu, 2241КБ)). Процессы сборки надмолекулярных комплексов при индуцированной самоорганизации, когерентность при взаимодействии макромолекул на масштабах нанометров и пикосекунд сопровождается генерацией и преобразованием химических сигналов, создающих информационную сеть в клетке. Анализу этой сети в модельных и реальных системах уделяется сейчас много внимания.

Проблема создания логичной концепции химического сигнала не нова, но удовлетворительной конструкции пока нет. Решить эту проблемы путем жесткой формализации, видимо, нельзя. К этому есть веские причины, которые нетрудно понять из проведенных выше рассуждений вокруг уравнения Шредингера для супермолекулы. Неожиданно удачным оказалось определение кляксы как случайного векторного поля (в диссертации все наброски теории кляксы были удалены, но подходы к описанию взаимодействия кляксы с промокашкой, оставлены).

Концепция химического сигнала должна базироваться на супермолекуле как логической основе геометрических и электронных структур, термодинамических и кинетических свойств, состояний агрегации, физических и химических преобразований, специфичности биологически важных взаимодействий, также как на экспериментальных и теоретических методах изучения этих свойств. Идея молекуляризации охватывает материалы от основ физических твердотельных устройств до всех отраслей химии, биологии и нанотехнологии.
Молекулярные свойства определяют химический сигнал только в определенных пределах. Сюда относятся: структура нежестких молекул, свойства, согласующиеся с принципом неопределенности без учета квантового поля и релятивистских эффектов. Кроме того, существуют свойства, специфически зависящие от состояния агрегации, такие как сверхпроводимость, ферроэлектричество, сверхтекучесть и т.д. Очевидно, что любое определение коллективных молекулярных эффектов в проявлениях химического сигнала может потребоваться в более сложных случаях. При современном стремительном развитии молекулярной нанотехнологии можно ожидать, что идеи молекуляризации и концепция химического сигнала будут полезны для развития представлений по самоорганизации и представления новых идей по самосборке.

Следуя Колмогорову и используя понятие алгоритмической сложности рассмотрим кляксу как случайное векторное поле. Сложность 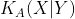$K_A (X|Y)$ кляксы 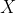$X$ относительно кляксы 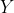$Y$ есть минимальная длина программы, перерабатывающей кляксу 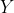$Y$ , который представлен в виде конечной двоичной последовательности, в двоичную последовательность 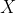$X$ , когда минимизация длины программы происходит по всем возможным универсальным методом программирования 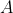$A$ . Предполагается, что нам удалось адекватно представить кляксу в виде большого двоичного объекта. Такое определение корректно в силу теоремы: существует универсальный метод программирования 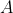$A$ , представляющий собой частично рекурсивную функцию и минимизирующий сложность кляксы 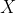$X$ относительно кляксы $Y$ .

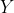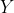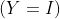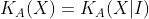Если $Y$ единичная клякса $(Y = I)$ , то $K_A (X) = K_A (X|I)$ есть сложность кляксы 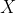$X$ . Количество информации, содержащейся в 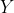$Y$ относительно 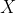$X$ , дается следующей формулой

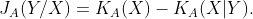$J_A (Y/X) = K_A (X) - K_A (X|Y).$ (1)

Другими словами 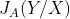$J_A (Y/X)$ есть сложность восстановления по фиксированной эталонной кляксе 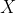$X$ при условии, что дана клякса $Y$ .
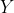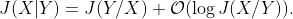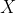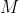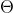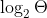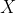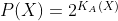Справедливо такое соотношение $J(X|Y) = J(Y/X) + {\cal O}(\log J(X/Y)).$ Элемент $X$ конечного множества $M$ мощности $\Theta$ считается случайным, если его сложность близка к $\log_2 \Theta$ . Вероятность натолкнуться на некоторую фиксированную кляксу $X$ задается так: $P(X)= 2^{K_A(X)}$ .
Используя формулу (1) запишем P(x) в другом виде:

$P(X) = 2^{-[J_A (Y/X) + K_A (X|Y)]}.$ (2)

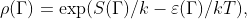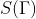Сопоставим (2) с функцией распределения $\rho(\Gamma)=\exp(S(\Gamma)/k - \varepsilon(\Gamma)/kT),$ где $S(\Gamma)$ - энтpопия, 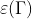$\varepsilon(\Gamma)$ - энеpгия, 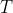$T$ - темпеpатуpа, 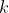$k$ - постоянная Больцмана. Из сопоставления 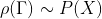$\rho(\Gamma) \sim P(X)$ получим следующие соответствия:

$S(\Gamma)/k <=> - J_A (Y/X); \qquad \varepsilon (\Gamma)/kT <=> K_A (X|Y).$
С учетом, что свободная энергия 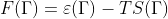$F(\Gamma) = \varepsilon(\Gamma) - TS(\Gamma)$ , можно сделать сопоставление 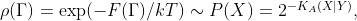$\rho(\Gamma)=\exp(-F(\Gamma)/kT) \sim P(X) = 2^{- K_A (X|Y)},$ из котоpого получаем искомое соответствие между алгоpитмической сложностью кляксы и ее свободной энеpгией

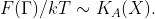
$F(\Gamma)/kT \sim K_A (X).$

Связь сложности и энтропии Колмогорова хорошо видна на дискретных отображениях, рассмотренных в 3 и 4 главах, из которых видно, что результат отображений представляет собой кляксу при динамическом хаосе. Можно предполагать существование потенциала кляксы или гармонической меры, аналогичной мере фрактала Мандельброта.

Peter Belobrov 31 Aug 2014 09:03