Мы как-то слабо развиваем наше понимание того, что обсуждение основных процессов в живых системах обязательно надо проводить на языке биологических переменных. Понятие взаимодействия не позволяет перейти на собственный язык биологии. Почему? Ответ прост! Применение физических и химических мер в биологии позволяет лишь "оцифровывать" биологическое действие переходя к биочислам (ссылки) количественной биологии. Математические меры надо модифицировать, чтобы правильно выражать содержательный смысл биологических утверждений. Конечно, биологическая математика потихоньку развивается, о чём скажем в другом месте.

Вот одна из главных биологических теорем. Биологическое действие никогда не равно биологическому противодействию, но их отличие является движущей силой развития.
Формула "Биологическое действие не равно противодействию, их отличие суть движущая сила развития" была озвучена в посте PIT00400.

Давно пора переходить от взаимодействия к биологическому действию. Понимание их принципиального отличия простым не будет. Почему? Причину можно усмотреть во внимательном чтении статей [Nel2009] и [Auffan2009]. На русском языке подробный реферат этих статей сделал Антон Чугунов на сайте biomolecula.ru 8/10/2010: Невидимая граница, где сталкиваются «нано» и «био».

Понимание нано-био взаимодействий - пост DIA00190 и

Вернёмся к биологическому действию.

{Nel2009} Andre E. Nel, Lutz Mädler, Darrell Velegol, Tian Xia, Eric MV Hoek, Ponisseril Somasundaran, Fred Klaessig, Vince Castranova, and Mike Thompson. Understanding biophysicochemical interactions at the nano-bio interface // Nature materials 8 (7), 543 (2009). doi 10.1038/nmat2442 Cited by 4669 (6/6/2019)

{Auffan2009} Mélanie Auffan, Mélanie Jerome Rose, Jean-Yves Bottero, Gregory V. Lowry, Jean-Pierre Jolivet, and Mark R. Wiesner. Towards a definition of inorganic nanoparticles from an environmental, health and safety perspective // Nature nanotechnology 4 (10), 634 (2009). doi 10.1038/nnano.2009.242 Cited by 1242 (6/6/2019)

Особый пост - особый текст. Здесь я поделюсь своими соображениями по поводу теоретической фундаментальной биологии. Конечно, рассматривать надо математическую, физическую, химическую и биологическую стороны Единой Природы. Выражаем это графически на рисунках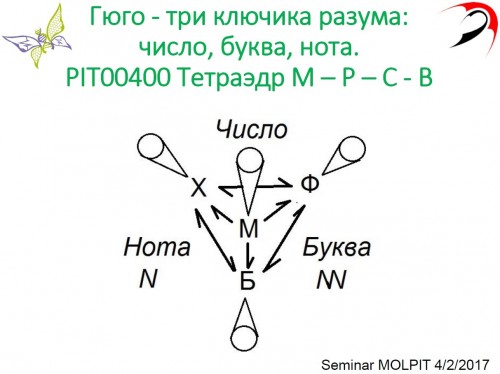

Используя латинские буквы для названия вершин получаем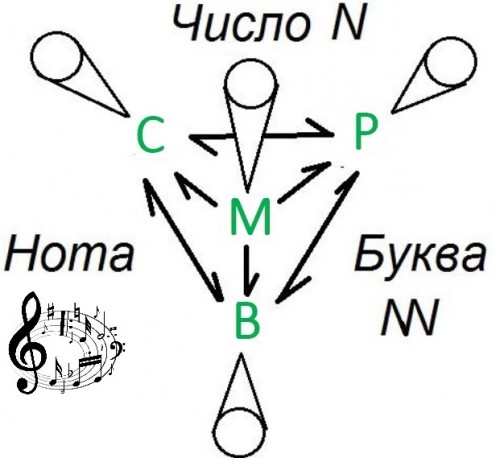

Особый символ NN – Non-Numbering, NN – символ для клякс и тучек.

4 вершины М (M), Ф (P), Х (C), Б (B); 4 грани МФХ (MPC), ФХБ (PCB), МФБ (MPB), МХБ (MCB); 6 ребер МБ (MB), МФ (MP), МХ (MC), БХ (BC), ХФ (CP), ФБ (PB). Многогранные конусы при каждой вершине обозначают все разделы каждой из "чистых" наук.

Важна цель – теория биологии

Понимание роли нечисловых переменных

Объект – организация живых систем, цель – создание фундаментальной биологии путём развития методов теоретической биологии.

Проблемы создания биологической математики

Множества не одинаковых элементов

Нечисловые объекты часто используются в математике, как-то: группы, топологии, пространства, но только при заданных заранее свойствах и одинаковости (однородности) переменных

При переходе к созиданию (рождению нового) из неодинаковых элементов возникает необходимость измеримости (построения теории мер) в нечисловых конструкциях

Биологическая алгебра

И, пожалуй, самое важное и самое трудное, измерение одного объекта другим без приведения к единой системе координат.

Это же отказ от глобального описания, когда нет «средней температуры по больнице» или же она бессмысленна

Для нечисловых величин возможно введение символов (букв, образов, клякс), хотя задавать их свойства заранее невозможно, они рождаются в процессе совместной экспрессии большого числа нечисловых объектов

Это как будто бы рождающаяся алгебра в полях взаимного действия различных объектов

Как рождается биологическая алгебра?

Действие не равно противодействию, их отличие суть движущая сила развития.

Да, это формула! Но сама по себе одна она не образует алгебры, кольца, поля или программы

Надо что-то добавить. Но что?

Наследование, генетику … это же опять сведение к одной переменной

Сложность, целостность, индивидуальность

Разнообразие конечных объектов, обеспечивающее непрерывность всего процесса созидания

Ребра тетраэдра M – P – C - B

МБ (MB), МФ (MP), МХ (MC)
Математическая биология
Биологическая математика

БХ (BC)
Биологическая химия
Химическая биология

ХФ (CP)
Химическая физика
Физическая химия

ФБ (PB)
Физическая биология
Биологическая физика

Понимание роли нечисловых переменных

Грани тетраэдра M – P – C - B

МФХ (MPC)
Грань: математика – физика – химия

ФХБ (PCB)
Грань: физика – химия – биология

МФБ (MPB)
Грань: математика – физика – биология

МХБ (MCB)
Грань: математика – химия – биология

Теория организации живых систем. Цель – создание фундаментальной биологии путём развития методов теоретической биологии.

Вершины тетраэдра M – P – C - B

М (M)
Арифметика, алгебра, анализ, геометрия, топология …

Ф (P)
Теорфизика, механика, поля, частицы, кванты …

Х (C)
Алхимия, неорганика, органика, синтез, раствор …

Б (B)
Эмбриология, физиология, иммунология, генетика …

Основной объект – (само)организация в живых системах, цель – фундаментальная биология, подход – методы теоретической биологии

Непросто сделать формализм

Да!

А что если формализм содержательных систем?

Забавно, надо подумать

Комментируя сегодня дополнительно пост Ивана DIA00150, понял, что кроме ссылки на пост DIA00097, наверное, сам метод дополнительных частиц можно изложить независимо от предыдущих постов, т.е. в обычном, легко читаемом тексте, скажем так, пока препринта, например, "Метод дополнительных частиц при точном описании сложных взаимодействий". При этом даже не надо будет акцентировать внимания на биологические частицы, а можно взять чисто абстрактное взаимодействие.

Продолжая через неделю (21/12/14), удалось, наконец, определить логику текста этого препринта.

Начать надо будет с медиатора (mediator) как способа описания взаимного действия через среду (medium), затем введение точного значения действия () с последующим описанием локального (точечного) взаимодействия, затем появление ядерных сил не зависящих от расстояния, взаимодействие через поля действия, квантование которых и привело к представлению о кванте поля как о переносчике (mediate) взаимодействия при возрастании сложности взаимного действия от точечных (локальных) сил до полевых нелокальных, андронных, барионных, даже струнных действиях, порой странным образом зависящих (и даже не зависящих) от расстояния при более высоких энергиях в физике элементарных частиц.
Примечание 14/7/2018. 23/2/2017 был написан пост PIT00400 с формулой "Биологическое действие не равно противодействию, их отличие суть движущая сила развития".

На этом основании дополнительные частицы в модели Денисова можно рассматривать как кванты полей действия в сложных структурах, переносящих (mediate) нелокальные действия объектов на одном уровне организации. Тогда вопрос о том, какие свойства дополнительные частицы наследуют от объектов (частиц) данного уровня, а какие свойства появляются, т.е. их не было у частиц данного уровня, становится количественным и вычисляемым.

Таким образом, дополнительные частицы в модели Денисова, возникшие благодаря перепутыванию смысла слов mediate и transfer, можно достаточно логично обосновать и применять для описания сложных взаимодействий, по-видимому, включая биологические, химические, коллоидные, энтропийные, дипольные и многие другие силы без обязательного введения абстрактных полей вместе с их квантованием. Например, гравитационное взаимодействие не удаётся проквантовать более 80 лет, т.е, видимо, гравитоны как кванты гравитационного поля не существуют в природе. К сожалению, физики в русском языке не ввели медиатор для квантов поля взаимодействия частиц и поэтому "переносчики взаимодействия" долго "морочили голову" тем, кто хотел понять единую суть гравитационного и биологического взаимодействий.

Рождение этой теории сложных взаимодействий обозначено временем 21/12/14 5:26К. Сейчас лишь добавлю то, что мне говорил Владимир Львович Галкин в студенческие годы: "если ты сделаешь правильную теорию самоорганизации, то она будет описывать даже элементарные частицы".

В статье [1] изложены и проанализированы обстоятельства появления работы Матвея Петровича Бронштейна 1935 года о квантовании гравитации — в контексте истории физики и научной биографии автора. В этом первом глубоком исследовании проблемы Бронштейн, анализируя измеримость поля, обнаружил «принципиальное различие между квантовой электродинамикой и квантовой теорией гравитационного поля» и выявил принципиальную трудность соединения ОТО и квантовой теории. Среди явных и неявных участников истории — М. Планк, А. Эйнштейн, В. Гейзенберг, В. Паули, Л. Розенфельд, Л. Ландау и Н. Бор. Обсуждается методологическая уникальность проблемы квантования гравитации, так и не решенной за истекшие 70 лет. Добавлю, уже 80 лет! А теперь прочтите тексты [2, 3] Матвея Петровича через призму дополнительных частиц ... попытайтесь, хотя бы ...

Дополнение 9/4/2015. После обсуждения поста PIT00201 мне стало понятно, что над темой этого поста я непрерывно размышлял в течение 3-х месяцев, что выражено на открытой странице http://molpit.org/?page=46 (повторю ссылку здесь bmp150330corr150409 (pdf, 3148КБ)) названием моей презентации "Квантование нелокальных гравитационных и биологических полей в клетке".

Литература

[1] Горелик Г Е. Матвей Бронштейн и квантовая гравитация. К 70-летию нерешенной проблемы r0510d (pdf, 875КБ) // УФН 175 1093–1108 (2005)

[2] Bronstein M "Quantentheorie schwacher Gravitationsfelder" Phys. Z. Sowjetunion 9 140 - 157 (1936); Бронштейн М Эйнштейновский сборник, 1980 - 1981 (Отв. ред. И Ю Кобзарев, Сост. Г Е Горелик) (М.: Наука, 1985) 1935p267-282 (djvu, 4235КБ) с. 267 - 282.

[3] Бронштейн М П "Квантование гравитационных волн" ЖЭТФ 6 195 - 236 (1936). см с. 433 - 445 1936p433-445 (djvu, 9900КБ) в Куранский Е С (Ред.) Альберт Эйнштейн и теория гравитации. Сб. статей (М.: Мир, 1979)